There are several methods which can be used to determine the fix in coastal navigation. These can also be combined with translation of previously known position lines and /or combined with celestial navigation position lines. Some of these methods are very accurate, placing you on the chart to within a few metres, others are less accurate but simpler.
The methods are:
Two bearings. This requires two conspicuous objects on shore.
45° and Abeam. A single object is required for this method. You must maintain a fixed course over the period.
Doubling the angle on the Bow. Similar method as above but less accurate.
Two angles to shore objects. Requires 3 objects on shore. If angles are measured by sextant, very high accuracy can be obtained.
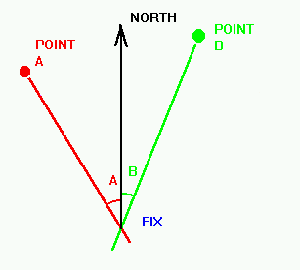
This is the simplest and most obvious way to get a fix. Find two objects along the coast, which are clearly indicated on the chart, take a bearing on each, plot the bearings on the chart (don't forget about the magnetic variation, and any other deviation caused by your vessel). Where the two bearing lines meet is where you are.
Two Bearings
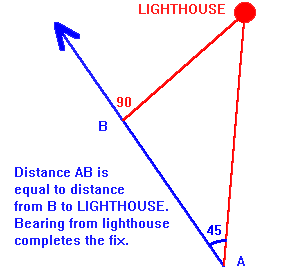
This is an easy and reasonably accurate method to ascertain one's position when a single object is available on shore. Simply read the log when the object is bearing 45° from the direction of travel (don't forget to allow for leeway and current drift) . Read the log again when the same object is abeam (ie 90° from the direction of travel). The difference between the two log readings is the distance between the object and you. A bearing from the object will complete the fix as you know the distance from the object.
45° and Abeam
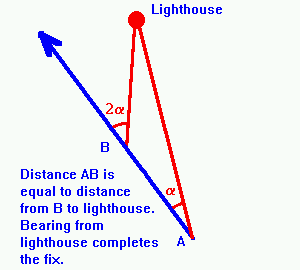
This is a generalised version of the 45°/Abeam method. Again a single object is available on shore. Simply read the log when the object is bearing any angle alpha from the direction of travel. Read the log again when the same object is bearing twice the original angle. The difference between the two log readings is the distance between the object and you. The bearing from the object will complete the fix as you know the distance from the object.
Double the angle
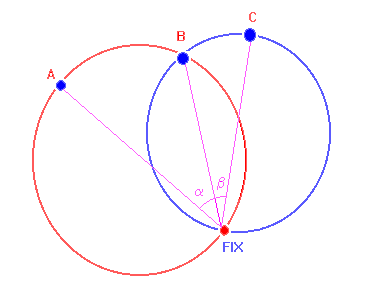
The angles seen between 3 shore objects allow two circles to be drawn on the chart. The intersection of the circles will yield your fix to a very high precision. The angles can be measured by sextant to a very high accuracy and it is one of the less well known use of a sextant but not any less useful. Now those of you who did not fall asleep during the geometry lessons will remember that all the points which see another two fixed points with the same subtended angle are all on the same circle (which also passes by the two fixed points). As for those who did fall asleep, or thought maths were a waste of time and of no practical use, well : " get lost then, or go back to school". The following figure shows how to construct the circle from the angle masurement between two objects A and B.
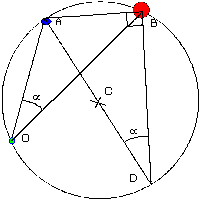
With three objects, two angles can be obtained, and two circles. The intersection giving the fix. If only two objects are available, then draw the circle and get the fix from the bearing of the nearest object (to minimise the errors).
Two Circles
| Rhumb Lines |  |
