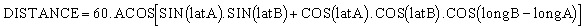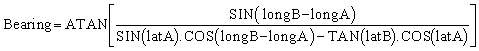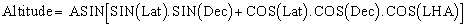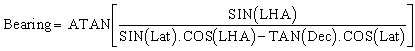Celestial navigation has been with us since the beginning of time.
Various civilizations have used it, some like the Polynesians, with
remarkable and extremely daring skills. What follows is a set of
mathematical formulas which I have derived over the years for my own
use. All the formulas published here are based on equations which I
have solved myself, none were copied from any other books. This does
not mean that I did not read books on celestial navigation, merely
that I read them after having solved the problems my own way. Nor are
these formulas readily found as most navigational text books are
guides telling you how to use other publications (eg HO249) which let
you find the result without any calculations. This is all well and
good, but it won't let you program your own calculator.
So this
page is for the people who are curious, have a table of logarithms
(the batteries never run out on these and I certainly haven't thrown
mine out) or a scientific calculator.
Definitions of terms
The first thing to learn are the terms. In this page I shall follow the sailor's convention though I will mention in passing, when and if I think about it, the astronomer's and land surveyor's terms.
Celestial navigation is based on 2 spheres. One is the earth, and I guess everybody knows that the coordinates to be used are the latitude and longitude. Celestial objects have a similar set of coordinates however, two such sets are in use at the same time: One set is called longitude and latitude, these refer to the position relative to the ecliptic plane which is the plane of the Earth's orbit around the Sun and which is tilted about 23° relative to the equatorial plane, in this system, the origin of all coordinates is the centre of the Sun.
The other system is essentially an earth centered view of the universe and uses a set of coordinates based on the equatorial plane. The coordinates in this system are the declination and the Greenwich hour angle.
Declination : This marks the height above or below the equatorial plane for celestial objects. Equivalent to the latitude on earth. it is followed by North or South same as latitude.
GHA : GHA (Greenwich Hour Angle) indicates the position past the plane of the Greenwich meridian measured in degrees. Equivalent to longitude on earth. It can be followed by East or West.
LHA : LHA (Local Hour Angle) is the angle between the meridian of the celestial object and the meridian of the observer, LHA = GHA(of celestial object) - Longitude (of observer).
SHA : Sidereal Hour Angle. Because the fixed stars (they are not really fixed, but they are so far away that they don't seem to move much), don't move relative to each other, rather than give the GHA of each star for each hour of the day, for each day of the year, the Nautical Almanac publishes only the list of GHA for a fictitious point called "first point of Aries" (also denoted by the Zodiac sign of the Ram). The SHA of the stars is simply a coordinate relative to this point. So to calculate the GHA of a star all you have to do is: GHA(star) = SHA(star) + GHA(aries). Ideally the GHA of aries should not vary relative to the stars, unfortunately, as Hipparchus noted a long time ago, the earth wobbles, its axis doing a full circle in about 26000 years (if my memory is correct) which means that the first point of Aries slowly drifts across the background of stars, making a full circle in 26000 years. It is called the first point of aries because it is the point where the sun crosses the equatorial plane on its way from the southern hemisphere to the northern one (around the 21st of March) and it happens to fall in the Zodiac sign of Aries the Ram. Will the point change name when it has drifted into another sign? Well the answer to this one is already known as the drift has already occured and the 1st point of Aries is actually in Pisces at the moment but we still call it 1st point of Aries. Old habits die hard.
Note that astronomers and land surveyors use RA (Right Ascension) instead of SHA, usually measured in time (hours and minutes) and increasing in an Easterly direction, to convert just remember that 1hour=15 degrees, 1 minute of time = 15 minutes of arc and don't forget to change the sign. Instead of GHA Aries they use GST (Greenwich Sidereal Time).
Ecliptic : Plane where lies the orbit of the earth. From our view point, the path defined by the sun as it travels over the year and therefore the plane where the Zodiac signs lay. Most planets also are in this plane to a close approximation which makes me wonder how Kepler decided that the orbit of the planets around the sun was elliptical rather than circular when all he could see was a circle almost edge on.
Altitude or Elevation : Angle between a celestial body and the horizontal plane of the observer, as measured by a sextant for sailors and theodolites for surveyors.
Equinoctial Plane : Plane defined for the celestial sphere to separate the Northern part from the Southern part. Since this plane is merely an extension of the equatorial plane, it's obviously a deliberate attempt by astronomers to confuse us by giving 2 names to the same plane.
Azimuth : Angle measured horizontally between the direction of the nearest pole and the vertical plane where lies the celestial object (ie if the object is north of you then it is the angle between true north and the object, if it's south then it's the angle between true south and the object) . I don't use it myself as I am easily confused and I prefer to use the bearing which is always measured from true North and goes clockwise (0 = North, 90 = East, 180 = South 270= West, 360=0=North). If you are wise, you'll use the bearing as well, but if you use pre compiled tables such as HO249, then you will have to use the azimuth.
Bearing : Angle measured horizontally from North to whatever direction you are pointing. Since there are 2 norths, the TRUE north and the MAGNETIC North, then specify the figures by saying TRUE bearing or MAG. bearing. This way you won't confuse anyone (including yourself). And remember the sailor's motto :
" If the variation is West,
the compass is best.
If the variation is East,
the compass is least"Nautical Mile : Officially, a nautical mile is defined as 1852 m or 6080 feet. But originally it was a minute of arc on a great circle. It is the 2nd definition that we will use here here, as do every sailor around the world, thereby showing the standard makers what we really think of them.
Sign convention : Because my formulas are meant to be universal, these are the sign conventions which I have adopted. Others may have used different sign convention, that's their prerogative but I don't care.
Latitude and Declination will be positive when North, negative otherwise.
Longitude, GHA, SHA, and LHA will be positive when West, negative when East.
Bearings will always be positive when measured clockwise, negative when anticlockwise.
Note also that in my formulas, I've assumed for angle of arc unit the degree, hence why the number 60 appears sometimes to convert degrees into minutes (or nautical miles since 1 nautical mile = 1 minute of arc on the earth).
Distance and bearing between 2 points on earth
Suppose you are at point "A", latA and longA being the latitude and longitude of A, and you want to know how far point B is ( latB, longB ). The distance in Nautical miles is:
And the bearing angle of B as seen from A is given by:
Now this formula, I have never seen in any book, what I have seen is an ACOS function of the azimuth. But in my view an ATAN function is preferable as it at least gives you the correct direction. OK so you might end up travelling in the opposite direction and circle the great circle from the long side rather than the short one, but at least you will arrive at B eventually. With the ACOS formula, it is possible to pick the wrong great circle (the one with the symmetrical azimuth) . If you do, you'll never ever meet B.
These 2 formulas can come in pretty handy also if you want to erect the tourist direction pointers which have about 50 indicators mounted on a post, all pointing in a different direction, and reading: "New-York 4622 miles", "Tokyo 2473 miles", etc.., your signs will point to the right directions and have the correct distances (at least they will before vandals come and rearrange the lot).
Find also the handy Great Circle calculator which lets you do the calculation easily.
Altitude and Bearing of a Celestial Object
Suppose now that you know where you are (eg Lat and Long are known) and there is a celestial body which you are about to observe and whose coordinates you know (Dec and GHA), is it possible to predict what elevation you will measure and what the bearing to the object is? The answer is yes to both questions. First calculate the local hour angle, LHA = GHA - Long (remember the sign convention, whilst the nautical almanac only publishes positive GHA's, it is customary to refer to an eastern longitude as a positive number. Melbourne's longitude is about 150 E but this is equivalent to -150 W or 210 W, therefore in this case LHA = GHA + 150 or LHA = GHA - 210, either formula is correct). Then we get for the altitude:
And the bearing is given by :
Do these formulas look familiar ?
Well they should because they are identical to the distance and bearing formulas presented earlier, the idea behind celestial navigation is to calculate the distance and bearing from yourself to the point on earth directly below the celestial object which you observe, except that the sextant, instead of measuring the angle between you and the celestial object as seen from the centre of the earth, measures the complementary angle because we use the horizon instead of the vertical as a reference. Therefore ASIN appears in the formula instead of ACOS. Again the ATAN formula for the bearing is better than the ACOS or ASIN form. For instance if the formula is based on the ACOS function, and you are taking a sun sight around lunch time and your azimuth is returned as Az=ACOS(0.97) does that mean the Azimuth is 14 degrees or is it -14 degrees (ie is the Sun a little bit to the East or a little bit to the West), easy to make a mistake. With ASIN, the problem arises early in the morning (is the Sun a little bit South or a little bit North of East) and in late afternoon (is the Sun a little bit North or a little bit South of West). Hard to tell sometimes without having to think about it. With the ATAN formula, no thinking required, the Sun is either North or South at lunch time but, unless it is dead over head, I know which it is . In the morning it can only be East (West does not make sense then) , in the evening it can only be West (East does not make sense now).
Navigation in principle
Of course, if you already know where you are, there is no point in trying to determine it from the formulas above . But when you actually navigate, the odds are you don't know quite where you are, so how do we use the above formulas?
We draw what is called a position line or Sumner line. Although the modern position line is not quite a real Sumner line but it is close enough.
Like all good inventions, Sumner lines were discovered by chance by a fellow called , you guessed right, "Sumner", Thomas H. Sumner to be precise (maybe related to the late professor Julius Sumner-Miller). Sumner was a ship captain on his way from Charleston (South Carolina) to Greenock (Scotland). And he was worried because he had been sailing for several days in bad weather, the wind was blowing from the South East making Ireland a lee shore, and he had not been able to see the sun or any stars, the coast was getting near, and he did not know exactly where he was. Suddenly there was a break in the clouds, so he grabbed his sextant and snatched a quick sun sight, before the clouds covered the sky again.
Now he was wondering what to do with this information so he played a "what if" game. He did not use the bearing formula above, because nobody had worked it out in quite that form yet, but he knew the altitude formula and he said "what if my latitude is... " and calculated the corresponding longitude and he plotted it on the chart, then he tried it again with another latitude, got another point on the chart. After doing that three or four times he suddenly realised that all the points he was marking on the chart seemed to fall on a straight line. Without thinking about it any more, he saw that the line needed pushing north by a few odd miles to lead straight over Small's light, so he turned north for those few miles, then turned to starboard until he was sailing parallel to that very first "Sumner line". His crew were a bit perplexed at that, wondering if the captain had gone mad, but when suddenly they arrived right at the very light, they thought he was a flaming genius. And so did the rest of the sailing community.
So why did the points fall on a straight line? They did not really but Sumner did not realise it at the time. The points Sumner was plotting were the points on earth from which any one would have seen, at the same moment as he did, the sun with exactly the same altitude. All those points are on a circle centered at the point on earth directly below the sun. Because this circle is usually huge, a small part of it appears straight on a Mercator projection chart.
So this is how we proceed in practice:
We assume we know where we are , we call this DR (for Dead Reckoning).
We calculate, based on the latitude and longitude of the DR, what the bearing and the altitude of the celestial object would be at the time of observation.
We draw the bearing line passing through DR.
We compare the actual measured altitude, with what it would have been had we been at DR, the difference, in minutes of arc, is equal to the number of nautical miles that we have to move along the bearing line to find our position line. ie if the angle measured is greater than the calculated one by say 13' of arc, then we move towards the celestial object by 13 nautical miles, and if say the measured angle was less by 7' of arc than the calculated one, we would move away from the celestial object by 7 nautical miles.
Finally we draw a line at right angle to the bearing line, passing by the point we have just found. This line is our position line and all we can tell is we are somewhere on this line.
Note the difference between our position line and Sumner's original one: our line is the tangent to the circle at the point nearest to DR, Sumner's was the circle. Sumner's line is in theory more accurate, but the circle is usually so large that the loss of accuracy is insignificant. Note also that in the tropics the circles can be extremely small, I remember reading about a P&O captain who used to obtain all his fixes without any calculation, he would take several observations when the sun was nearly dead overhead (say over a 15 minute period) for each time observation, he would plot the coordinates (GHA,DEC) of the Sun on his map then draw a circle of radius equal to (90 degrees - measured altitude). Since over the 15 minute period he would probably have collected 4 or 5 observations, he would draw 4 or 5 circles which would all intersect at one point. Simple but effective especially as in the tropics, position lines usually end up running all almost North-South giving good longitude information but lousy intercepts and large errors in latitude. The noon sight is damn important then.
If you wait a few hours, the sun will change position and you will be able to repeat the operation and determine a 2nd position line which will intersect the first. Provided you haven't moved in the interval, you are at the intersection.
If you have moved (and the odds are you would because it can be pretty boring sitting around doing nothing on a boat that's just bobbing up and down in the middle of the ocean), then all you need do is translate the original position line in the same direction, and the same distance as you have travelled. Your position will be at the intercept of the new line and the translated one. Sailors call this the SUN-RUN-SUN method.
| Navigation Index |  |
 |
Sextant Corrections |