2nd Puzzle Answer

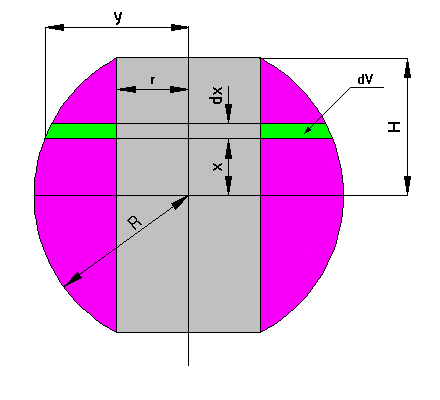
If we call H the dimension from the centre of the sphere to one of the flat ends, R the sphere radius, r the cylindrical hole radius and x the distance from the centre of the sphere to some plane normal to the cylinder axis (refer attached picture). This plane intersects the sphere at a distance y from the axis.

Using Pythagoras's theorem we have:

r² = R² - H²
y² = R² - x²

The volume dV between the plane at x and that at x + dx is :

dV = PI * ( y² - r² ) * dx

Replacing y² and r² by their value above, we get:

dV = PI * ( H² - x² ) * dx

Obviously this shows that the volume is independent of R and depends on H only, if one makes R decrease to H then the internal cylinder decreases in volume and at the limit it becomes 0 when the sphere radius is equal to H

The answer therefore is V = 4/3 PI * H³ . It is also the simplest way I know to prove that the volume of a sphere is 4/3 PI * R³, simply integrate dV (very simple) then make H tend to R.

V = 36 Pi cubic centimetres.

Back to Puzzle Page