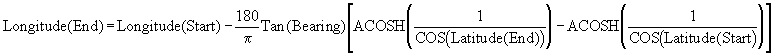
The process of map making is a complicated process. The dilemma is how to show on a flat piece of paper a surface which is originally spherical.
Archimedes's demonstration of the surface of a sphere being equal to that of the cylinder surrounding it exactly and of height equal to the sphere diameter (yes it was Archie who did it first, anticipating in the process Newton's calculus by 1800 years or so) can be used for instance to show a mapping process where the areas are all conserved accurately. If I had to show a map of the world where areas of countries have to be of the correct value, I would probably use Archimedes's method despite the horrible distortions which would occur in the high latitudes (the vertical axis being squashed flatter and flatter as one approaches the North Pole, whilst the horizontal axis is stretched. The result conserving the area within any closed contour)
The navigator's needs are somewhat different, it does not matter to him whether areas are conserved, directions are more important. Archimedes's method is useless for this as, apart from North-South, and East-West, all other directions are modified. Mercator's projection solves this mapping problem. Mercator's is also a cylindrical projection, but the vertical scale is modified in such a way that , within a relatively small area of the map, the dimensions have the same scale in the N-S and E-W direction, this trick ensures that any directional vector will have the same direction (bearing) on the map, as it has on the earth. Since the longitude scale has to be constant (in degrees) for north to always point north, the vertical scale has to be expanded inversely to the cosine of latitude. One degree of latitude at a latitude of 60 degrees, will therefore be twice as large as at the equator (because cos(60) = 1/2).
The early navigators soon gave up great circle navigation ("orthodromie" en français) as a bad joke when they realised that, when sailing along a great circle, the bearing changes constantly. They soon decided that sailing along a constant bearing, whilst perhaps taking a little longer, was far simpler. You just measured the bearing on the Mercator's chart, and this was the bearing to follow to go where you wanted to go.
This line of constant bearing is called a Rhumb line. The word "rhumb" (or sometimes rumb and it is the same in French though not very well known) comes from the name of angle measurement representing the "point" on the old fashioned compass cards. There are 32 "rhumbs" in 360 degrees, hence a rhumb is 11 1/4 degrees.
When sailing along a rhumb line at a particular bearing, B, the change of latitude is simple to calculate, if L is the distance travelled, then L.COS(B) is the change in latitude (remember the sign convention: if COS(B) is negative, the change is southerly, if positive, northerly).
Things are more complicated for the change in longitude. The sailors call departure, D, the value D=-L.SIN(B) (don't forget the - sign, a bearing less than 180 always sends you travelling eastward. And don't complain to me, if I had had anything to do with it, compass cards would have a graduation running anticlockwise in the proper trigonometric direction), and use the approximate relation : Change in Longitude = D/COS(Latitude).
The problem, and therefore the reason why the formula is approximate, is which latitude do you use. That of the original point? or the one of the final point? or the one of some intermediate point?. Well the correct answer is always that of one (sometimes either one of two) intermediate points. This is really a question which never truly bothers sailors. When a good day's run is likely to be no more than 240 nautical miles (most would be happy with half that but some speed maniacs have multihulls just so on a good day they can beat the 200 miles limit) and therefore a change in latitude is always less than 3 degrees. Considering all the other errors produced by leeway, currents, that of choosing the "wrong" latitude is rather insignificant. Besides if you use a proper chart for plotting, you don't need to calculate anything, just plot and make sure you scale your units on the right part of the chart.
But there are the purists (and those with programmable calculators like myself) who would prefer a "correct" formula. So here we go:
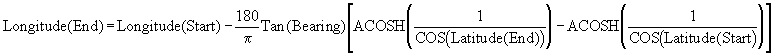
Of course ACOSH is also called COSH-1 on some calculators. It is the inverse hyperbolic cosine function.
Where did I get this one from you say? well I made it up which was easy once I had proven the following integral:
It looks simple doesn't it. This simple integral only took me several years to solve. No! not continuously, maybe 10 minutes once every couple of months, long enough each time to get nowhere. And then one day I said it must be possible and I gave it my undivided attention for a few hours and suddenly Eureka. Of course, I still had taken a wrong start (and I also probably took the wrong turn at Albuquerque) and ended up travelling through the complex number domain, but I got there in the end. And I can't see what was so hard when I look at how simple it is ... now that I know.
If your calculator does not have a COSH or ACOSH function, write a program to calculate them :
COSH(x) = ( ex + e-x )/2
Here is a handy little calculator, licensed under the GPL, to quickly calculate rhumb lines bearings and distances.
| Sextant Errors And Corrections |  |
 |
Conning and Pilotage |